* 다익스트라(Dijkstra) 알고리즘

한 정점에서 다른 정점으로 가는 최단거리를 구하는 알고리즘으로 가중치가 음수면 사용이 불가능하다.

다익스트라는 최단거리는 최단거리들로 이루어져 있다는 Greedy한 아이디어로 만들어진 알고리즘이다.

주로 우선순위 큐와 BFS를 이용하여 구현되며, 작동 방식은 다음과 같다.

1. 아직 방문하지 않은 정점들 중 거리가 가장 짧은 정점을 하나 선택해 방문한다.

2. 해당 정점에서 인접하고 아직 방문하지 않은 정점들의 거리를 갱신한다.

* 작동 예시

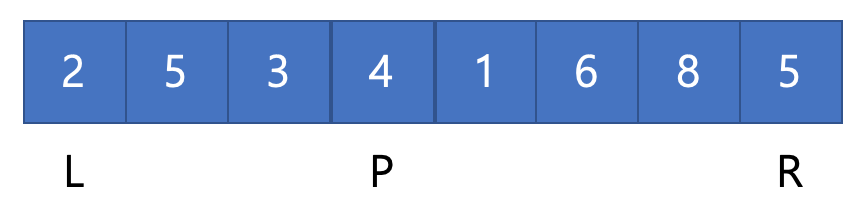
0번 정점에서 시작한다고 가정하고, 위와 같은 그래프가 있을 때 작동방식은 다음과 같다.

위 순서를 통해 정점과 정점사이의 최단 거리를 구한다.

핵심은 최단거리는 최단거리들로 이루어져 있다는 생각이고, 선택한 정점과 인접한 최소한의 가중치를 가진 간선을 선택하는 것은 프림 알고리즘과 비슷하다.

하지만, 프림 알고리즘과 달리 우선순위 큐에 해당 가중치를 계속 더해가며 최단 경로를 찾는 알고리즘이다.

백준/1753 :: 최단경로 문제

백준/1753 :: 최단경로 풀이

* 합병 정렬(Merge Sort)    =>O(nlogn)

합병 정렬은 O(nlogn) 의 시간복잡도를 보장한다.

하지만 단점은 임시 배열 공간이 추가로 필요하다는 점이다.

분할 정복으로 구현하는데, 배열을 최대한 나누고 각 배열을 다시 정렬하면서 합병하는 방식이다.

< 작동 방식 >

1. 나눌 수 있는 만큼 끝까지 나눈다. (1개가 될때까지)

2. 나누어진 배열을 임시 배열에 저장하고 이를 비교하면서 확인한다.

모든 작동방식을 알아보는 것 보다 합치는 과정에 대표적인 예를 통해 작동방식을 알아보자.

우선 배열을 하나의 배열까지 쪼갠 후 합치면서 정렬한다.

이후 tmp 배열에 4개의 data를 복사한다.

left = start, right = mid+1로 설정하고 서로 비교해 작은 값을 data에 덮어씌운다.

left를 한칸 이동하고 작은 값을 data에 덮어씌운다.

right를 한칸 이동하고 작은 값을 data에 덮어씌운다.

right가 배열의 끝에 도달했기 때문에 남은 left를 data에 덮어씌운다.

이런 방식으로 통해 정렬하는 방식이다.

추가로, 이 방식은 left가 남았을 때만 남은 data를 덮어 씌워주면 되는데, 그 이유는 처음 시작때 임시 배열에 data를 복사했기 때문이다.

아래 예시를 살펴보자.

tmp에 data를 복사한 후 left와 right를 비교해 작은 값을 data에 넣는다.

left를 한칸 이동하고 작은 값을 data에 덮어 씌운다.

여기서 Right에 있는 값을 굳이 덮어 씌우지 않아도 원본 데이터랑 같기 때문에 Right의 경우 덮어씌울 필요가 없다.

< 소스 코드 >

* 퀵 정렬(Quick Sort)    =>평균 O(nlogn), 최악 O(n^2)

자바에서 Arrays.sort를 사용하변 내부는 Quick Sort로 구현되어있다.

평균 O(nlogn) 이지만 최악에 O(n^2) 이므로 데이터가 많은 경우 조심해야 한다.

최악의 경우란 아이러니하게도 정렬된 경우를 의미한다.

< 작동 방식 >

퀵 정렬은 pivot값을 중심으로 왼쪽에는 pivot 보다 작은 값들, 오른쪽에는 pivot보다 크거나 같은 값을 정렬한다.

기준을 잡고, left, right 포인터를 이동하면서 num[left] > pivot 과 num[right] < pivot 인 경우 서로 교환한다.

소스 코드와 그림으로 이해하자.

num[left] > pivot, num[right] < pivot 조건을 만족할 때까지 left, right를 움직인다.

pivot을 가운데 값으로 설정하고 Left, Right 를 각 끝의 idx를 지정한다.

< 소스 코드 >

버블 정렬(Bubble Sort)

• 인접한 두 숫자를 비교해서 변경하는 방법
• 오른쪽부터 최대값/최소값을 정렬해 나가는 방식

1 2 3 4 5 6 7

public void BubbleSort(int[] num) { for (int i = 0; i < num.length; i++) { for (int j = 1; j < num.length - i; j++) { if (num[j] < num[j - 1]) swap(j - 1, j, num); } } }

---

선택 정렬(Selection Sort)

• 자신보다 뒤에있는 숫자들 중 가장 작은 숫자를 발견해서 맨 앞에서부터 채우는 정렬
• 왼쪽부터 최대값/최소값을 정렬해 나가는 방식

1 2 3 4 5 6 7 8 9

public void SelectionSort(int[] num) { for (int i = 0; i < num.length; i++) { int min = i; for (int j = i + 1; j < num.length; j++) { if (num[min] > num[j]) min = j; } if (num[min] < num[i]) swap(min, i, num); } }

---

삽입 정렬(Insertion Sort)

• i번째 배열 값부터 앞으로 탐색하며 자신보다 작다면 swap하는 정렬
• n번째 수행시 n번째 까지 정렬되는 방법

1 2 3 4 5 6 7 8 9 10 11

public void InsertioinSort(int[] num) { for (int i = 1; i < num.length; i++) { int tmp = num[i]; for (int j = i - 1; j >= 0; j--) { if (tmp < num[j]) { num[j + 1] = num[j]; num[j] = tmp; } } } }

---

퀵 정렬(Quick Sort)

• pivot을 정하고 pivot 좌/우를 정렬하면서 전체 배열을 정렬
• 자바에서 Arrays.sort를 사용하변 내부는 Quick Sort로 구현되어있다.
• 평균 O(nlogn) 이지만 최악에 O(n^2) 이므로 데이터가 많은 경우 조심해야 한다.
• 최악의 경우란 아이러니하게도 정렬된 경우를 의미한다.

< 작동 방식 >

• pivot을 가운데 값으로 설정하고 Left, Right 를 각 끝의 idx를 지정한다.

• num[left] > pivot, num[right] < pivot 조건을 만족할 때까지 left, right를 움직인다.

• 둘의 위치를 바꾼다. 이렇게 되면 pivot 왼쪽에는 pivot보다 작은 값, 오른쪽에는 큰값이 정렬된다.

< 소스 코드 >

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

public int partition(int left, int right, int[] num) { int pivot = num[(left + right) / 2]; while (left <= right) { while (num[left] < pivot) left++; while (num[right] > pivot) right--; if (left <= right) { swap(left, right, num); left++; right--; } } return left; } public void QuickSort(int left, int right, int[] num) { if (left < right) { int pivot = partition(left, right, num); if (left < pivot - 1) QuickSort(left, pivot - 1, num); if (right > pivot) QuickSort(pivot, right, num); } }

---

합병 정렬(Merge Sort)

• 합병 정렬은 O(nlogn) 의 시간복잡도를 보장한다.
• 단점은 임시 배열 공간이 추가로 필요하다는 점이다.
• 분할 정복으로 구현하는데 배열을 최대한 나누고, 합병하면서 값을 비교해 정렬하는 방식이다.

< 작동 방식 >

1. left = start, right = mid+1로 설정하고 서로 비교해 작은 값을 data에 덮어씌운다.
2. left를 한칸 이동하고 작은 값을 data에 덮어씌운다.
3. right를 한칸 이동하고 작은 값을 data에 덮어씌운다.
4. right가 배열의 끝에 도달했기 때문에 남은 left를 data에 덮어씌운다.

< 소스 코드 >

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

public void mergeSort(int start, int end) { if (start < end) { int mid = (start + end) / 2; mergeSort(start, mid); mergeSort(mid + 1, end); merge(start, mid, end); } } public void merge(int start, int mid, int end) { for (int i = start; i <= end; i++) { tmp[i] = num[i]; //tmp 배열에 값을 옮긴다. } int left = start; int right = mid + 1; int idx = start; while (left <= mid && right <= end) { //num 배열에 비교하면서 저장 if (tmp[left] >= tmp[right]) { num[idx++] = tmp[right++]; } else { num[idx++] = tmp[left++]; } } //어느 한쪽에 남은 tmp 배열을 num 배열에 저장 while (left <= mid) num[idx++] = tmp[left++]; while (right <= end) num[idx++] = tmp[right++]; }

* 개념 이해

공통 부분 문자열과 최장 공통 부분 수열은 비슷한점이 많다.

공통 부분 문자열(Longest Common Substring)은 중간에 끊어지는 값이 이어지는 부분 배열중에서 문자열을 찾는 방식이고,

최장 공통 부분 수열(Longest Common Subsequence)은 문자열이 연속되지 않아도 선택이 가능하다.

위와 같은 예시가 있을 때,

공통 부분 문자열은 BCD, 최장 공통 부분 수열은 BCDEF 가 될 것이다.

* 공통 부분 문자열

문자열 A와 B가 있을 때,

dp[i][j] = A문자열은 i번째, B문자열은 j번째 글자까지 비교했을 때 가장 긴 공통 부분 문자열의 길이

DBC와 ABC를 비교했을 때 공통 부분 문자열은 BC가 있으므로 답은 2가 될 것이다.

이를 코드로 구현하면 다음과 같다.

* 최장 공통 부분 수열(Longest Common Subsequence) 

문자열 A와 B가 있을 때, 

dp[i][j] = A문자열은 i번째, B문자열은 j번째 글자까지 비교했을 때의 최장 공통 부분 수열의 길이

예를 들어, ABCD와 BACD를 비교한다고 생각해보자.

(3,3) 값을 보면 2라는 값이 나오는데, 이는 BAC와 ABC를 비교한 값이다. 

dp에는 이전 까지 저장된 최장 공통 부분 수열의 길이를 저장하고 A문자열 i번째와 B문자열 j번째가 같으면 +1을 해주면 된다.

A문자열 i번째와 B문자열 j번째가 같지 않더라도 이전까지 구한 값이 최장 공통 부분 수열이기 때문에 (i-1,j)와 (i,j-1) 중에서 최대값을 저장하면 된다.

만약, LCS의 문자열을 구해야 한다면, (i,j)부터 회색으로 색칠된 부분의 문자열만 추가하는 방식으로 진행하면 될 것이다.

이를 코드로 구현하면 다음과 같다.

* 세그먼트 트리

배열이 주어졌을 때 해당 배열을 완전 이진 트리 Leaf Node에 넣고 Leaf Node의 부모 노드에 합/곱/Max/Min을 올려가는 방식이다.

A 배열의 부분 합을 구할때 배열의 값이 변하거나 테스트 케이스가 많을 경우(쿼리가 많을 경우) 시간 복잡도가 한 쿼리당 O(logN)으로 계산할 수 있다.

* 세그먼트 트리에서 값을 저장하는 방식

부모 노드가 n 번째 노드라면 n*2, n*2+1 번째 노드를 자식노드로 가진다는 특성을 이용하여 1차원 배열에 저장한다.

처음 입력받는 값들은 Leaf Node이기 때문에 뒤쪽 배열에 값을 저장하고,

자식노드가 n 번째 노드라면 n/2 번째 부모 노드에 트리방식에 따라 합/곱/Max/Min을 저장한다. 이 때의 시간복잡도는 O(logN)이다.

Leaf Node의 값을 변경하게 된다면 트리방식에 따라 부모 노드들을 수정하면 된다. 이때 시간 복잡도는 O(logN)이 된다.

* 소스 코드

출처 : https://www.codeground.org/

* 참고 문제

백준/2042 :: 구간 합 구하기

백준/1275 :: 커피숍2

* 최단 경로 알고리즘

최소 신장 트리와 달리, 최단 경로 알고리즘은 출발 정점과 도착 정점이 존재한다.

즉, 최소 신장 트리처럼 모든 정점을 방문할 필요 없이 출발 정점에서 도착 정점까지 최단 경로만 찾으면 된다.

* 다익스트라 알고리즘    =>O(|E||log|V|)

1. 출발 지점에서 시작하는 간선들 중 최소 가중치를 가지는 간선을 선택한다.

2. 해당 정점을 방문하면 해당 정점까지 필요한 가중치 + 해당 정점에서 방문할 수 있는 간선의 가중치 들을 우선순위 큐에 넣는다.

3. 위 과정을 목표 정점에 도착할 때까지 반복한다.

단, 음의 가중치가 존재해서는 안된다. => 벨만-포드 알고리즘 사용

* 벨만 - 포드 알고리즘    =>O(VE)

* 플로이드 와샬 알고리즘    =>O(n^3)

모든 경우의 수를 시도해보는 알고리즘이다.

2차원 배열 d의 초기값을 모두 무한대로 설정한다.

이후 해당 정점을 거쳐가는 최단거리가 있다면 해당 거리를 업데이트한다.

즉, d[1][5] = d[1][k] + d[k][5]가 되는데 

d[1][1] + d[1][5]  or  d[1][2] + d[2][5]  or  d[1][3] + d[3][5]  or  d[1][4] + d[4][5]  or  d[1][5] + d[5][5] 중 최소값을 찾는다.

* MST란?

Minimum Spanning Tree의 약자로, 직역하면 최소 신장 트리라고 불린다.

Spanning Tree는 모든 정점들이 연결 되어 있어야 하고 사이클을 포함해서는 안된다.

앞에 Minimum을 붙이면 각 간선의 가중치가 다른 경우 최소의 가중치로 연결하여 모든 정점을 방문하는 것을 말한다.

즉, MST에서는 간선의 가중치가 최소로 모든 정점을 방문해야하며 사이클이 생겨서는 안된다.

MST에는 크게 Kruskal(크루스칼) 알고리즘과 Prim(프림) 알고리즘이 존재한다.

* 크루스칼 알고리즘 (+Union-Find)

1. 간선을 가중치에 따라 오름차순으로 정렬한다. (Comparable 사용)

2. 가장 가중치를 가지는 간선을 첫번째 간선으로 선택한다.

3. 가중치가 작은 간선을 선택한다.

4. 선택한 간선과 이전에 선택한 간선이 사이클을 이루는지 확인한다. (Union-Find(Disjoint-Set) 사용)

Union-Find 자료구조에서 Disjoint-Set 확인 방법은 다음과 같다.

1. 초기화 : N 개의 원소가 각각의 집합에 포함되어 있도록 초기화 합니다. 

2. Union (합치기) 연산 : 두 원소 a, b 가 주어질 때, 이들이 속한 두 집합을 하나로 합칩니다. 

3. Find (찾기) 연산 : 어떤 원소 a 가 주어질 때, 이 원소가 속한 집합을 반환합니다. 

즉, disjoint를 통해 같은 집합여부를 확인할 수 있다.

이를 소스코드로 표현하면 다음과 같다.

백준/1922 :: 네트워크 연결 문제

백준/1922 :: 네트워크 연결 풀이

* 프림 알고리즘 

1. 가중치가 낮은 간선을 선택한다.

2. 선택한 간선과 인접한 간선 중에서, 사이클을 생성하지 않는 간선 중에서 가중치가 작은 간선을 선택한다. (현재 간선의 가중치를 추가하면 다익스트라)

3. 위 과정을 반복하여 n-1개의 간선을 선택한다.

위 과정을 거치기 때문에 간선을 선택할 때마다 트리의 형태가 유지된다. (보통 우선순위큐를 이용하여 BFS로 구현한다.)

프림 알고리즘은 다익스트라(Dijkstra) 개념과 같이 이해하는게 편리하다.

cf) 프림 알고리즘 : MST를 만들 때 사용하는 알고리즘으로 BFS처럼 선마다 최소 가중치를 찾아 연결하는 방법

다익스트라 알고리즘 : 시작 정점 x에서 도착 정점 y까지 최단거리로 이동하는 방식