* 합병 정렬(Merge Sort)    =>O(nlogn)

합병 정렬은 O(nlogn) 의 시간복잡도를 보장한다.

하지만 단점은 임시 배열 공간이 추가로 필요하다는 점이다.

분할 정복으로 구현하는데, 배열을 최대한 나누고 각 배열을 다시 정렬하면서 합병하는 방식이다.

< 작동 방식 >

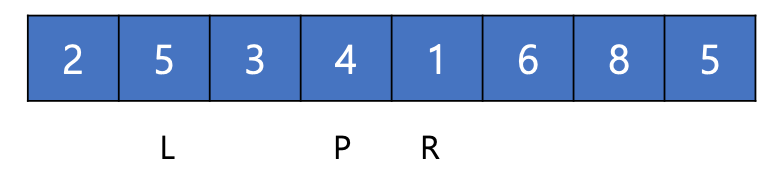
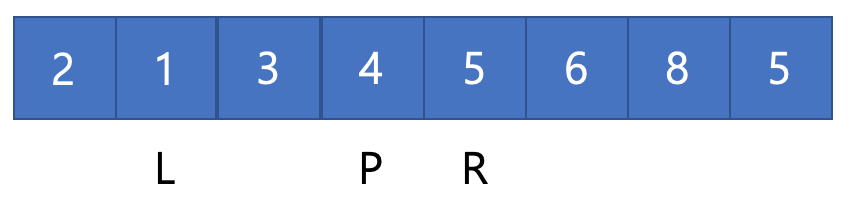
1. 나눌 수 있는 만큼 끝까지 나눈다. (1개가 될때까지)

2. 나누어진 배열을 임시 배열에 저장하고 이를 비교하면서 확인한다.

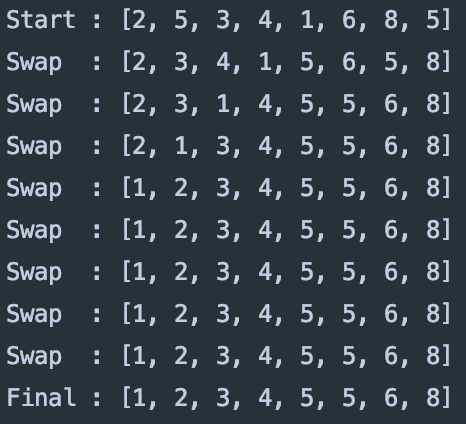
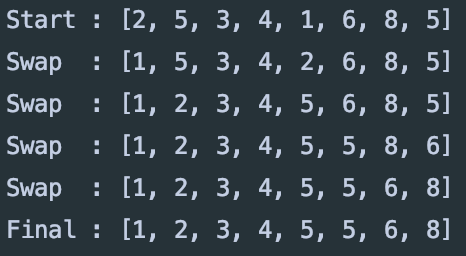
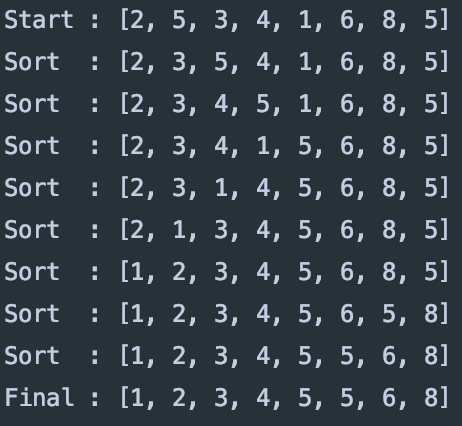
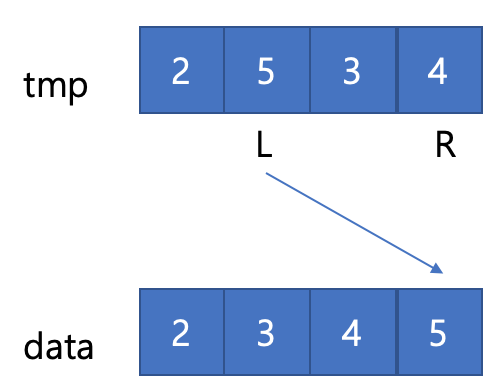
모든 작동방식을 알아보는 것 보다 합치는 과정에 대표적인 예를 통해 작동방식을 알아보자.

우선 배열을 하나의 배열까지 쪼갠 후 합치면서 정렬한다.

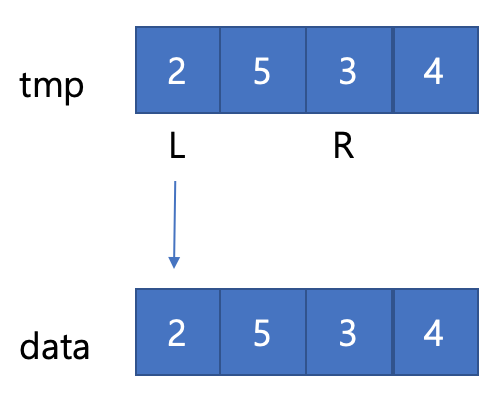
이후 tmp 배열에 4개의 data를 복사한다.

left = start, right = mid+1로 설정하고 서로 비교해 작은 값을 data에 덮어씌운다.

left를 한칸 이동하고 작은 값을 data에 덮어씌운다.

right를 한칸 이동하고 작은 값을 data에 덮어씌운다.

right가 배열의 끝에 도달했기 때문에 남은 left를 data에 덮어씌운다.

이런 방식으로 통해 정렬하는 방식이다.

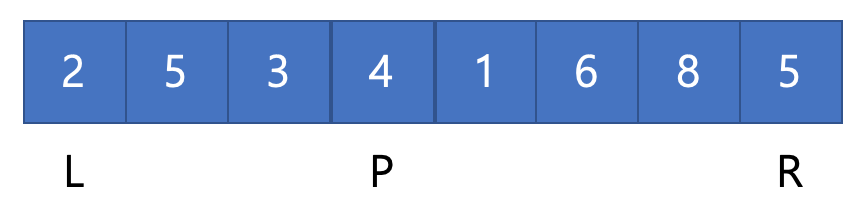
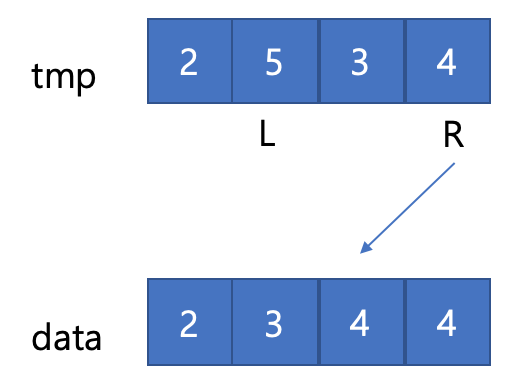
추가로, 이 방식은 left가 남았을 때만 남은 data를 덮어 씌워주면 되는데, 그 이유는 처음 시작때 임시 배열에 data를 복사했기 때문이다.

아래 예시를 살펴보자.

tmp에 data를 복사한 후 left와 right를 비교해 작은 값을 data에 넣는다.

left를 한칸 이동하고 작은 값을 data에 덮어 씌운다.

여기서 Right에 있는 값을 굳이 덮어 씌우지 않아도 원본 데이터랑 같기 때문에 Right의 경우 덮어씌울 필요가 없다.

< 소스 코드 >

* 퀵 정렬(Quick Sort)    =>평균 O(nlogn), 최악 O(n^2)

자바에서 Arrays.sort를 사용하변 내부는 Quick Sort로 구현되어있다.

평균 O(nlogn) 이지만 최악에 O(n^2) 이므로 데이터가 많은 경우 조심해야 한다.

최악의 경우란 아이러니하게도 정렬된 경우를 의미한다.

< 작동 방식 >

퀵 정렬은 pivot값을 중심으로 왼쪽에는 pivot 보다 작은 값들, 오른쪽에는 pivot보다 크거나 같은 값을 정렬한다.

기준을 잡고, left, right 포인터를 이동하면서 num[left] > pivot 과 num[right] < pivot 인 경우 서로 교환한다.

소스 코드와 그림으로 이해하자.

num[left] > pivot, num[right] < pivot 조건을 만족할 때까지 left, right를 움직인다.

pivot을 가운데 값으로 설정하고 Left, Right 를 각 끝의 idx를 지정한다.

< 소스 코드 >

버블 정렬(Bubble Sort)

• 인접한 두 숫자를 비교해서 변경하는 방법
• 오른쪽부터 최대값/최소값을 정렬해 나가는 방식

1 2 3 4 5 6 7

public void BubbleSort(int[] num) { for (int i = 0; i < num.length; i++) { for (int j = 1; j < num.length - i; j++) { if (num[j] < num[j - 1]) swap(j - 1, j, num); } } }

---

선택 정렬(Selection Sort)

• 자신보다 뒤에있는 숫자들 중 가장 작은 숫자를 발견해서 맨 앞에서부터 채우는 정렬
• 왼쪽부터 최대값/최소값을 정렬해 나가는 방식

1 2 3 4 5 6 7 8 9

public void SelectionSort(int[] num) { for (int i = 0; i < num.length; i++) { int min = i; for (int j = i + 1; j < num.length; j++) { if (num[min] > num[j]) min = j; } if (num[min] < num[i]) swap(min, i, num); } }

---

삽입 정렬(Insertion Sort)

• i번째 배열 값부터 앞으로 탐색하며 자신보다 작다면 swap하는 정렬
• n번째 수행시 n번째 까지 정렬되는 방법

1 2 3 4 5 6 7 8 9 10 11

public void InsertioinSort(int[] num) { for (int i = 1; i < num.length; i++) { int tmp = num[i]; for (int j = i - 1; j >= 0; j--) { if (tmp < num[j]) { num[j + 1] = num[j]; num[j] = tmp; } } } }

---

퀵 정렬(Quick Sort)

• pivot을 정하고 pivot 좌/우를 정렬하면서 전체 배열을 정렬
• 자바에서 Arrays.sort를 사용하변 내부는 Quick Sort로 구현되어있다.
• 평균 O(nlogn) 이지만 최악에 O(n^2) 이므로 데이터가 많은 경우 조심해야 한다.
• 최악의 경우란 아이러니하게도 정렬된 경우를 의미한다.

< 작동 방식 >

• pivot을 가운데 값으로 설정하고 Left, Right 를 각 끝의 idx를 지정한다.

• num[left] > pivot, num[right] < pivot 조건을 만족할 때까지 left, right를 움직인다.

• 둘의 위치를 바꾼다. 이렇게 되면 pivot 왼쪽에는 pivot보다 작은 값, 오른쪽에는 큰값이 정렬된다.

< 소스 코드 >

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

public int partition(int left, int right, int[] num) { int pivot = num[(left + right) / 2]; while (left <= right) { while (num[left] < pivot) left++; while (num[right] > pivot) right--; if (left <= right) { swap(left, right, num); left++; right--; } } return left; } public void QuickSort(int left, int right, int[] num) { if (left < right) { int pivot = partition(left, right, num); if (left < pivot - 1) QuickSort(left, pivot - 1, num); if (right > pivot) QuickSort(pivot, right, num); } }

---

합병 정렬(Merge Sort)

• 합병 정렬은 O(nlogn) 의 시간복잡도를 보장한다.
• 단점은 임시 배열 공간이 추가로 필요하다는 점이다.
• 분할 정복으로 구현하는데 배열을 최대한 나누고, 합병하면서 값을 비교해 정렬하는 방식이다.

< 작동 방식 >

1. left = start, right = mid+1로 설정하고 서로 비교해 작은 값을 data에 덮어씌운다.
2. left를 한칸 이동하고 작은 값을 data에 덮어씌운다.
3. right를 한칸 이동하고 작은 값을 data에 덮어씌운다.
4. right가 배열의 끝에 도달했기 때문에 남은 left를 data에 덮어씌운다.

< 소스 코드 >

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

public void mergeSort(int start, int end) { if (start < end) { int mid = (start + end) / 2; mergeSort(start, mid); mergeSort(mid + 1, end); merge(start, mid, end); } } public void merge(int start, int mid, int end) { for (int i = start; i <= end; i++) { tmp[i] = num[i]; //tmp 배열에 값을 옮긴다. } int left = start; int right = mid + 1; int idx = start; while (left <= mid && right <= end) { //num 배열에 비교하면서 저장 if (tmp[left] >= tmp[right]) { num[idx++] = tmp[right++]; } else { num[idx++] = tmp[left++]; } } //어느 한쪽에 남은 tmp 배열을 num 배열에 저장 while (left <= mid) num[idx++] = tmp[left++]; while (right <= end) num[idx++] = tmp[right++]; }