[Algorithm Tech] 정렬 알고리즘

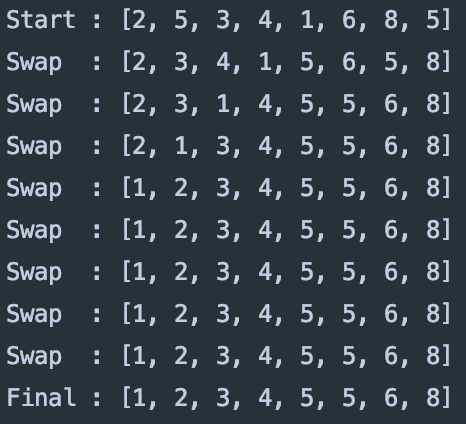
버블 정렬(Bubble Sort)

• 인접한 두 숫자를 비교해서 변경하는 방법
• 오른쪽부터 최대값/최소값을 정렬해 나가는 방식

1 2 3 4 5 6 7

public void BubbleSort(int[] num) { for (int i = 0; i < num.length; i++) { for (int j = 1; j < num.length - i; j++) { if (num[j] < num[j - 1]) swap(j - 1, j, num); } } }

---

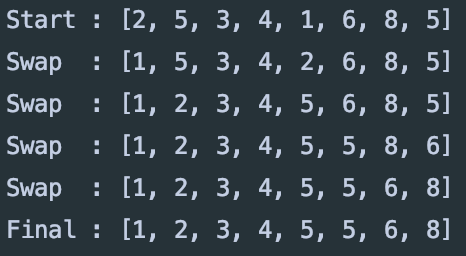
선택 정렬(Selection Sort)

• 자신보다 뒤에있는 숫자들 중 가장 작은 숫자를 발견해서 맨 앞에서부터 채우는 정렬
• 왼쪽부터 최대값/최소값을 정렬해 나가는 방식

1 2 3 4 5 6 7 8 9

public void SelectionSort(int[] num) { for (int i = 0; i < num.length; i++) { int min = i; for (int j = i + 1; j < num.length; j++) { if (num[min] > num[j]) min = j; } if (num[min] < num[i]) swap(min, i, num); } }

---

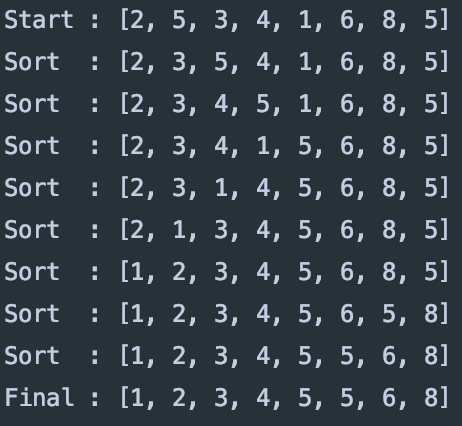
삽입 정렬(Insertion Sort)

• i번째 배열 값부터 앞으로 탐색하며 자신보다 작다면 swap하는 정렬
• n번째 수행시 n번째 까지 정렬되는 방법

1 2 3 4 5 6 7 8 9 10 11

public void InsertioinSort(int[] num) { for (int i = 1; i < num.length; i++) { int tmp = num[i]; for (int j = i - 1; j >= 0; j--) { if (tmp < num[j]) { num[j + 1] = num[j]; num[j] = tmp; } } } }

---

퀵 정렬(Quick Sort)

• pivot을 정하고 pivot 좌/우를 정렬하면서 전체 배열을 정렬
• 자바에서 Arrays.sort를 사용하변 내부는 Quick Sort로 구현되어있다.
• 평균 O(nlogn) 이지만 최악에 O(n^2) 이므로 데이터가 많은 경우 조심해야 한다.
• 최악의 경우란 아이러니하게도 정렬된 경우를 의미한다.

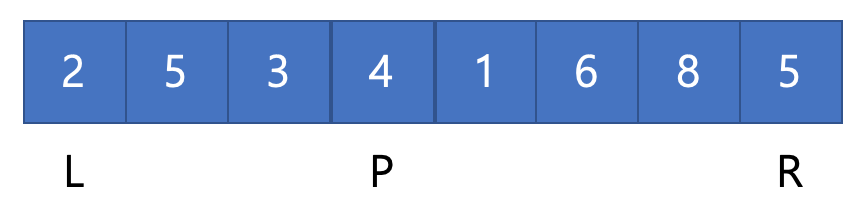
< 작동 방식 >

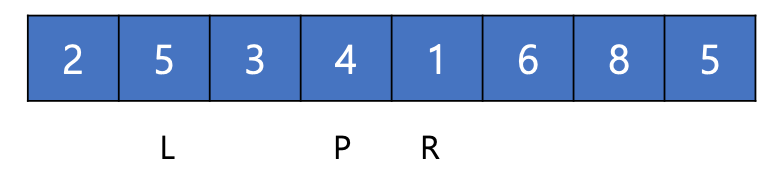
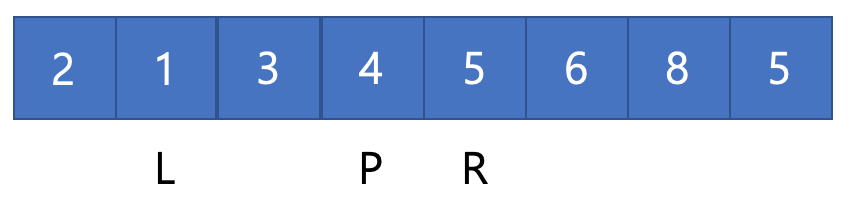
• pivot을 가운데 값으로 설정하고 Left, Right 를 각 끝의 idx를 지정한다.

• num[left] > pivot, num[right] < pivot 조건을 만족할 때까지 left, right를 움직인다.

• 둘의 위치를 바꾼다. 이렇게 되면 pivot 왼쪽에는 pivot보다 작은 값, 오른쪽에는 큰값이 정렬된다.

< 소스 코드 >

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

public int partition(int left, int right, int[] num) { int pivot = num[(left + right) / 2]; while (left <= right) { while (num[left] < pivot) left++; while (num[right] > pivot) right--; if (left <= right) { swap(left, right, num); left++; right--; } } return left; } public void QuickSort(int left, int right, int[] num) { if (left < right) { int pivot = partition(left, right, num); if (left < pivot - 1) QuickSort(left, pivot - 1, num); if (right > pivot) QuickSort(pivot, right, num); } }

---

합병 정렬(Merge Sort)

• 합병 정렬은 O(nlogn) 의 시간복잡도를 보장한다.
• 단점은 임시 배열 공간이 추가로 필요하다는 점이다.
• 분할 정복으로 구현하는데 배열을 최대한 나누고, 합병하면서 값을 비교해 정렬하는 방식이다.

< 작동 방식 >

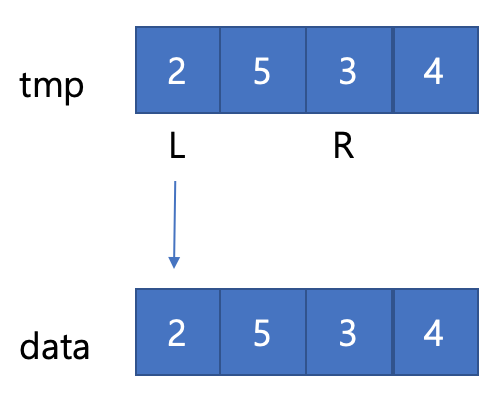
1. left = start, right = mid+1로 설정하고 서로 비교해 작은 값을 data에 덮어씌운다.
2. left를 한칸 이동하고 작은 값을 data에 덮어씌운다.
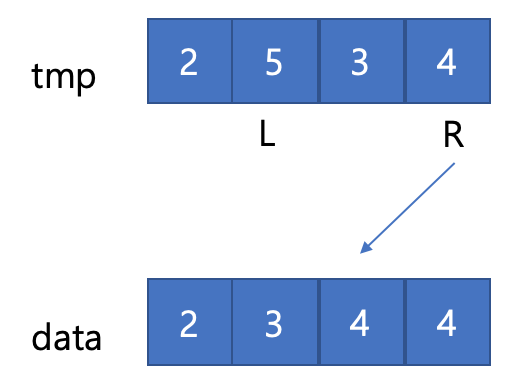
3. right를 한칸 이동하고 작은 값을 data에 덮어씌운다.
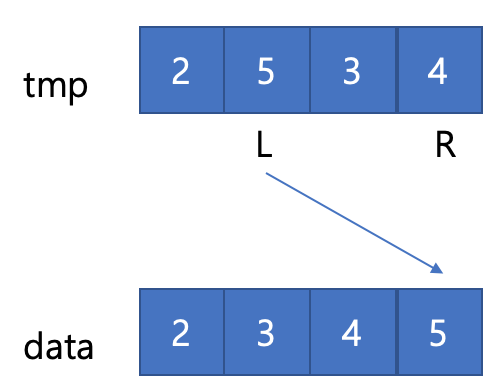
4. right가 배열의 끝에 도달했기 때문에 남은 left를 data에 덮어씌운다.

< 소스 코드 >

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

public void mergeSort(int start, int end) { if (start < end) { int mid = (start + end) / 2; mergeSort(start, mid); mergeSort(mid + 1, end); merge(start, mid, end); } } public void merge(int start, int mid, int end) { for (int i = start; i <= end; i++) { tmp[i] = num[i]; //tmp 배열에 값을 옮긴다. } int left = start; int right = mid + 1; int idx = start; while (left <= mid && right <= end) { //num 배열에 비교하면서 저장 if (tmp[left] >= tmp[right]) { num[idx++] = tmp[right++]; } else { num[idx++] = tmp[left++]; } } //어느 한쪽에 남은 tmp 배열을 num 배열에 저장 while (left <= mid) num[idx++] = tmp[left++]; while (right <= end) num[idx++] = tmp[right++]; }